AOE网

1.介绍
定义：在带权有向图中，以顶点表示事件，有向边表示活动，边上的权值表示完成该活动的开销，则称这种有向图为用边表示活动的网络，简称为AOE网（Activity On Edge Network）

性质：

• 只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始
• 只有在进入某一顶点的各有向边所代表的活动都已经结束时，该顶点所代表的事件才发生

2.几个词的解释
ps:事件是点，活动是边！！！

关键路径：
从源点到汇点的所有路径中，具有最长路径长度的路径，该路径上的活动成为关键活动（后面有用先记着）

事件V[k]的最早发生时间ve[k]:
从开始顶点V到V[k]的最长路径长度。

事件V[k]的最迟发生时间vl[k]:
不推迟整个工程完成的前提下，即保证它所指向的事件Vi在ve(i)时刻能够发生时，改事件最迟必须发生的事件。

活动a[i]的最早开始时间e[i]: 活动a[i]用边(V[k],V[j])表示

e[i]=ve[k]

活动a[i]的最迟开始时间l[i]:

l[i]=vl[j]-Weight(V[k],V[j])

一个活动a[i]的松弛时间：
d[i]=l[i]-e[i]或者d[i]=关键路径长度-包含a[i]活动的最长路径

3.计算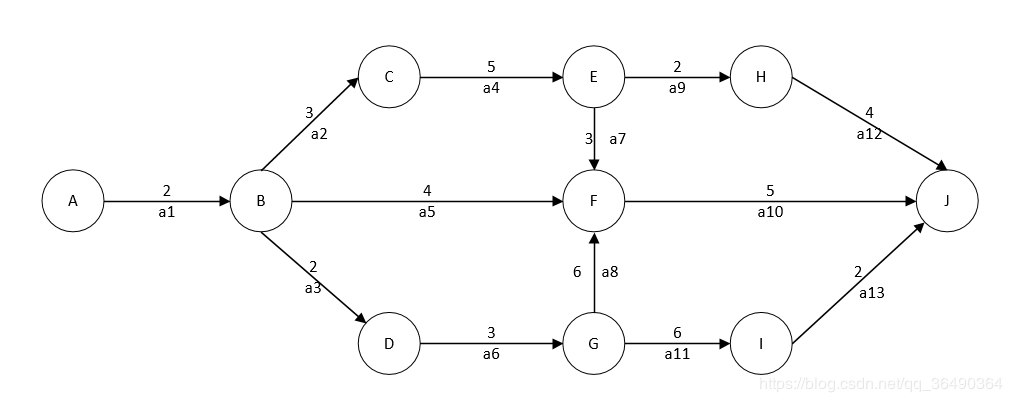

3.1 计算事件的最早和最迟发生时间

ve的计算方法为从前往后计算，取最大值，例如对于F,ve(F)=max{ve(B)+a5,ve(E)+a7,ve(G)+a8} ,只有一个的话就只取一个，多个的话，多个中取最大值

vl的计算方法为从后往前计算，首先另终点J的vl值为其ve，即vl(J)=ve(J)=18，然后多个中取最小值，例如对于B,vl(B)=min{vl(C)-a2,vl(F)-a5,vl(D)-a3}=2;若只有一个，例如对于H,vl(H)=vl(J)-a12=14

最终算出各个顶点的最早和最迟发生时间如下
|V|ve（事件最早发生时间）| vl（事件最迟发生事件）|
|—|—|—|
| A| 0 |0|
| B| 2 |2|
| C| 5 |5|
| D| 4|4|
| E| 10 |10|
| F|13 |13|
| G| 7 |7|
| H| 12 |14|
| I| 13 |16|
| J|18 |18|

有以上可以得出ve==vl的点即为关键路径上的事件，即A,B,C,D,E,F,G,J，则有以上点连接的边所代表的活动a1,a2,a3,a4,a6,a7,a8,a10疑似为关键活动
注意：
关键路径可能不只有一条，计算到这里只能得出关键路径上的事件，具体怎么走还等计算活动的最早和最迟开始时间，如果仅仅需要计算出关键路径，则只需计算几个疑似关键活动的最早和最迟发生时间，为了清楚，我们这里就把全部活动的都计算出来

3.2活动的最早和最迟开始时间
活动最早开始时间： 例如a1,为边（A,B），则a1=ve(A)=0;例如a2,为边（B,C），则a2=ve(B)=2

活动最晚开始时间：例如对于a1,为边（A,B）,则a1=vl(B)-weight(a1)=2-2=0；例如a12,为边（H,J）,则a12=vl(J)-weight(a12)=18-4=14

最终结果如下

a	e（活动最早开始时间）	l（活动最迟开始事件）
a1	0	0
a2	2	2
a3	2	2
a4	5	5
a5	2	9
a6	4	4
a7	10	10
a8	7	7
a9	10	12
a10	13	13
a11	7	10
a12	12	14
a13	13	16

找出e==l的活动ai,这里为a1,a2,a3,,a4,a6,a7,a8,a10;经观察可发现这里有两条关键路径，分别为a1,a2,a4,a7,a10和a1,a3,a6,a8,a10

又比如问一个活动的松弛时间，即活动ai在不拖延总工程时间的情况下，该活动可以拖延的时间，有两种解法，比如问BF的松弛时间：
解1：BF=a5,所以松弛时间=l(a5)-e(a5)=7
解2：包含BF活动的最长路径为ABFJ,其长度为11，又因为关键路径长度为18，所以松弛时间为18-11=7