1.推导

  (以下向量均为列向量)

  设平面$p_i$的法向量为$n_i$,$x_i$为该平面上任一点，则其在齐次坐标下的方程为：

$$\bar n_i=(n_i,-n_i \cdot x_i)$$

设空间中任意一点$x$的齐次坐标为$\bar x=(x, 1)$

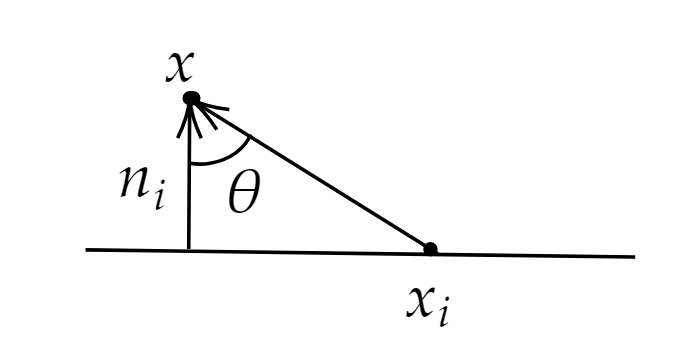
由几何关系可知$x$到$p_i$的距离的平方$d(x,p_i)$为：

$$\begin{align} d(x,p_i)&=((x-x_i)\cdot n_i)^2\\ &=(\begin{bmatrix}n_i,-n_i\cdot x_i\end{bmatrix}\begin{bmatrix}x\\1\end{bmatrix})^2\\ &=(\bar n_i^T\bar x)^2\\ &=\bar x^T(\bar n_i\bar n_i^T) \bar x\\ &=\bar x^TQ_i\bar x \end{align}$$

其中$Q_i$称为Quadratic error Matrix,注意到这个$Q_i$由于是法向量生成的，所以是定义面上的，现在分别定义顶点和边上的Quadratic error Matrix $Q_i^v$和$Q^e$:

$$\begin{align} Q_i^v&=\sum_{j\in \Omega(i)}Q_j\\ Q^e&=Q_1^v+Q_2^v \end{align}$$

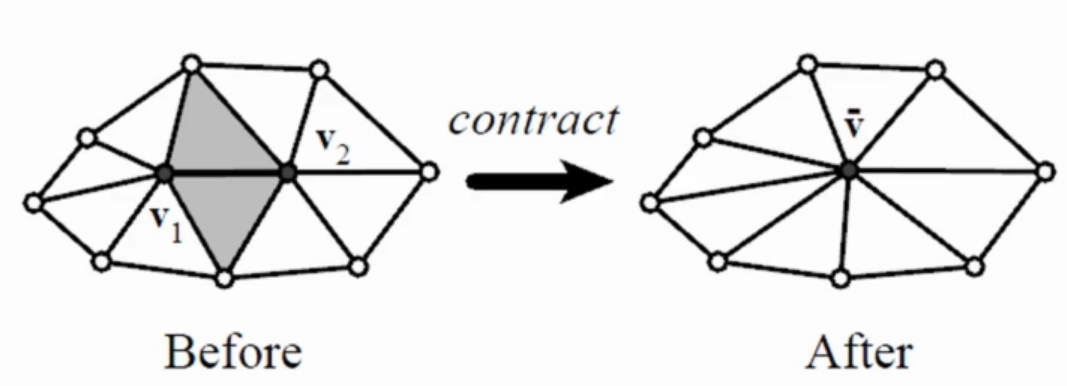
所以每条边上的 $\bar v$要满足

$$\bar v=min(v^TQ^ev)$$

若$Q^e$可逆，记$\Delta=v^TQ^ev$,当取最小值时，应该满足$\frac{\partial \Delta}{\partial x}=0$，$\frac{\partial \Delta}{\partial y}=0$，$\frac{\partial \Delta}{\partial z}=0$，即：

$$\left[\begin{array}{cccc} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{12} & q_{22} & q_{23} & q_{24} \\ q_{13} & q_{23} & q_{33} & q_{34} \\ 0 & 0 & 0 & 1 \end{array}\right] \mathbf{\mathbf { \bar v }}=\left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}\right]$$

（ps:如果$Q^e$不满秩，则可取$\bar v=\frac{v_1+v_2}{2}$,即为两顶点中点）

2. 算法流程

 输入：网格，目标定点数n，cost阈值t

 输出：简化后的网格

1. 计算每条边的 $Q^e$

2. 计算每条边上的新的$\bar v$

3. while $N_v$ >n and $Cost_{min}$<t:

   ​ 将每条边的$cost=\bar v^TQ^e\bar v$放入最小堆；

   ​ 删除堆顶的cost,并且塌陷该条边（即将该边的两个顶点并到$\bar v$上去，该新点上的Quadratic error Matrix则更新为刚才的$Q^e$）；

   ​ 更新堆(更新相邻的$Q^e$和cost)；

   end;