1.概括

  将3D中的标架场描述为Octahedral Fields：三维中所有旋转构成群特殊正交群$SO(3)$,但由于若只用向量表示，一个标架可有24个表示，其恰构成好八面体群$O$，因此若想唯一的标识标架，应该为$SO(3)/O$，而球谐基函数恰好可为其作代数表示。不同的是采用了边界元的思想，故而在求解中输入的网格只需要边界即可，如三角形网格，而不再是四面体网格。同时对于约束问题，之前采用对每个表面法向量对齐的方式，在这松弛为表面约束积分为面积常数。采用边界元后，输入网格不再需要四面体网格，同时可通过采样获取任意精度的内部标架。不过由于奇异提取也是通过采样，因此最终获得的是采样于奇异图的”奇异点云“，而这些采样在靠近边界处非常难获得(因为需要一个loop来包围它)。

2.解空间约束及松弛

  标架表示还是沿用球谐函数及九维向量表示。不同的是采用了边界元思想和新的约束表示。定义球谐基函数的系数集合如下，

$$\Gamma:=\left\{c \in \mathbb{R}^{9}: c=W_{4}(R) a_{0} \text { for some } R \in \mathrm{SO}(3)\right\} \subseteq \mathbb{R}^{9}$$

其中$\{W\in\mathbb{R}^{9 \times 9}: W^{\top} W=I_{9 \times 9}\}$，为Wigner-D matrix，因此$\Gamma$是单位化的。为了后续目标函数的优化，松弛单位化条件，将$\Gamma$中的元素设置成可缩放，如下

$$\bar{\Gamma}:=\{\beta c \in \Gamma: \beta \in \mathbb{R}\} \subseteq \mathbb{R}^{9}$$

不过需要注意的是$\bar{\Gamma}$是非线性，因此在使用边界元求解内部标架场过程中可能脱离$\bar \Gamma$，这意味着可能某些元素并不代表着正确的旋转，因此这时还需映射回（还是使用《Practical 3D Frame Field Generation》中的梯度下降法）$\bar{\Gamma}$。最后再通过单位化映射回$\Gamma$。

  可以注意到不是所有$\left\{c \in \mathbb{R}^{9}:\|c\|_{2}=1\right\}$中的向量都属于解空间$\Gamma$,如果不松弛这个条件，优化是非线性非凸的，这个是默认松弛了，最后会用梯度下降重新投影回来，即从九维重新映射回三维。

  至于单位化这个条件也是非凸的，如果用单位化向量去优化Dirichlet energy，如果存在奇异点，能量会blow up,尤其是在细分后，这个在《Globally Optimal Direction Fields》Section 3有提到。

  所以其实这里默认松弛了两个条件。

3.表面特征约束及松弛

  以上还是很抽象的解释，下面具体的约束表述。沿用过去球谐函数表示标架场的表面法向约束条件，定义如下

$$\begin{aligned} v_{c} &:=\sqrt{\frac{5}{12}}(0, \ldots, 0,1) \\ v_{s} &:=\sqrt{\frac{5}{12}(1,0, \ldots, 0)} \\ v_{n} &:=\sqrt{\frac{7}{12}}(0,0,0,0,1,0,0,0,0)\\ u_{\hat{n}}(\theta)&:=W_{4}\left(R_{\hat{n}}\right)\left[v_{n}+v_{c} \cos \theta+v_{s} \sin \theta\right] \end{aligned}$$

其中$W_{4}\left(R_{\hat{n}}\right)$是Wigner D-matrices，$R_{\hat{n}}$为将法向量旋转至Z轴的角度。进一步的，将边界约束写为如下形式，

$$\begin{aligned} u(x):=W_{4}&\left(R_{\hat{n}(x)}\right)\left[v_{n}+v_{c} c(x)+v_{s} s(x)\right]\\ &c^2(x)+s^2(x)=1 \end{aligned}$$

  该文的关键一步——将对每个标架的约束$c^2(x)+s^2(x)=1$，进一步松弛为表面积分形式，

$$\int_{\partial \Omega}\left[c(x)^{2}+s(x)^{2}\right] \mathrm{d} x=A$$

4.能量函数

  使用Dirichlet energy来平滑标架场，

$$E[u]:=\int_{\Omega}\|\nabla u(x)\|_{2}^{2} \mathrm{d} x=\int_{\partial \Omega}u\frac{\partial u}{\partial \hat n}$$

上述第二个等号的由来为：假设在内部$\Delta u=0$，使用格林第一恒等式。至此，可将能量函数的积分区域由$\Omega$转换为$\partial \Omega$。而对于$\frac{\partial u}{\partial \hat n}$,如果能从边界区域$\partial \Omega$得到，再加上边界上的约束条件，则能量函数可被我们真正计算出来。

  证明：根据格林第一恒等式

$$\int_{\Omega}(\nabla u\cdot \nabla v+u\Delta v)d\Omega=\int_\Gamma u\nabla v\cdot d\Gamma=\int_{\Gamma}u\frac{\partial v}{\partial n}d\Gamma$$

用$u$代替$v$,则

$$\int_{\Omega}(\nabla u\cdot \nabla u+u\Delta u)d\Omega=\int_\Gamma u\nabla u\cdot d\Gamma=\int_{\Gamma}u\frac{\partial u}{\partial n}d\Gamma$$

即

$$\int_{\Omega}||\nabla u||_2^{2}d\Omega=\int_{\Gamma}u\frac{\partial u}{\partial n}d\Gamma-\int_{\Omega}(u\Delta u)d\Omega$$

令$\Delta u=0$得到

$$\int_{\Omega}||\nabla u||_2^{2}d\Omega=\int_{\Gamma}u\frac{\partial u}{\partial n}d\Gamma$$

  对于$\frac{\partial u}{\partial \hat n}$,使用边界元的公式获得其与$u$的关系，

$$\frac{1}{2} u(x)=\int_{\partial \Omega}\left[G(y-x) \frac{\partial u(y)}{\partial \hat{n}}-u(y) \frac{\partial G(y-x)}{\partial \hat{n}}\right] \mathrm{d} y \quad\quad x\in \partial \Omega$$

其中$G(x)$是格林函数$\frac{1}{4\pi||x||}$。

1. 关于$\frac{\partial u}{\partial \hat n}$的计算是否可用$\nabla u \cdot \hat n$来完成？

2. 上面在化简Dirichlet energy到边界上时使用了条件$\Delta u=0$，而通过该条件也可使用分部积分反推出该能量函数。是否可直接使用拉普拉斯算子来平滑场，进而用拉普拉斯矩阵来优化？$\min_{x} \sum_{i, j} w_{i j}\left\|x_{i}-x_{j}\right\|_{2}^{2}=\min _{X}tr(X^TLX)$

  至此，能量函数归结为如下形式，

$$\begin{array}{l} \min _{u, \frac{\partial u}{\partial \hbar}, c, s} \quad E\left[u, \frac{\partial u}{\partial \hat{n}}\right]=\int_{\Omega}\|\nabla u\|_{2}^{2}=\int_{\partial \Omega} u \frac{\partial u}{\partial \hat{n}}\\ \text { s.t. }\quad u(x)=W_{4}\left(R_{\hat{n}(x)}\right)\left[v_{n}+v_{c} c(x)+v_{s} s(x)\right] \quad \forall x \in \partial \Omega \\ \int_{\partial \Omega}\left[c(x)^{2}+s(x)^{2}\right] \mathrm{d} x=A \\ \frac{1}{2} u(x)=\int_{\partial \Omega}\left[G(y-x) \frac{\partial u(y)}{\partial \hat{n}}-u(y) \frac{\partial G(y-x)}{\partial \hat{n}}\right] \mathrm{d} y \quad \text {holds} \quad \forall x \in \partial \Omega \end{array}$$

5.离散化

  假设网格为三角形网格，边界有$n$个面。每个面上有一个$u_k \in \mathbb{R}^{9}$，即表面上的标架存在于面上。定义$u\in \mathbb{R}^{9n}$为表面上的所有未知标架；定义$\bar{u}_{m} \in \mathbb{R}^{n}$为所有$u_k$的第$m$个系数,。根据已有的BEM方法(C. Pozrikidis - A Practical Guide to Boundary Element Methods with the Software Library BEMLIB §5.1.4 )可获得一个矩阵$B \in \mathbb{R}^{n\times n}$，则$\frac{\partial \bar{u}}{\partial \hat{n}}$可写成如下形式

$$B \bar{u}_{m} \approx\left(\frac{\partial \bar{u}}{\partial \hat{n}}\right)_{m}$$

  定义$\bar T$是一个关于网格单元面积的对角阵，定义$\bar L:=\bar T B$,在Dirichlet energy可离散化为

$$E\left[\left\{\bar{u}_{m}\right\}_{m=-4}^{4}\right]:=\sum_{m=-4}^{4} \bar{u}_{m}^{\top} \bar{L} \bar{u}_{m}=u^{\top} L u$$

其中$L \in \mathbb{R}^{9n\times 9n}$由$\bar L$这些分块组成，进一步如果$L$不对称，使其对称化,$L \leftarrow \frac{1}{2}\left(L+L^{\top}\right)$。（作者称$L$为半正定）

  定义$c,s \in \mathbb{R}^n$是边界上的约束，$u_0\in \mathbb{R}^{9n}$由$W_{4}\left(R_{\hat{n}_k}\right)v_n$分块组成，同时定义约束矩阵$H_c,H_s\in \mathbb{R}^{9n\times n}$分别为由$W_{4}\left(R_{\hat{n}_{k}}\right) v_{c} c_{k}$和$W_{4}\left(R_{\hat{n}_{k}}\right) v_{s} s_{k}$分块组成，则表面标架和表面法向约束变为

$$u=u_{0}+H_{c} c+H_{s} s\\ c^{\top} \bar{T} c+s^{\top} \bar{T} s=A$$

  至此，总的优化目标变为

$$\begin{aligned} \min _{\{u, c, s\}} & u^{\top} L u \\ \text { s.t. } & u=u_{0}+H_{c} c+H_{s} s \\ & c^{\top} \bar{T} c+s^{\top} \bar{T} s=A \end{aligned}$$

共有$9n+2n=11n$个变量，$9n+1$个约束，所以自由度$2n-1$。

6.优化

  定义如下矩阵

$$\begin{array}{l} Q:=\left(\begin{array}{cc} H_{c}^{\top} L H_{c} & H_{c}^{\top} L H_{s} \\ H_{s}^{\top} L H_{c} & H_{s}^{\top} L H_{s} \end{array}\right) \in \mathbb{R}^{2 n \times 2 n} \\ v:=\left(\begin{array}{c} H_{c}^{\top} L u_{0} \\ H_{s}^{\top} L u_{0} \end{array}\right) \in \mathbb{R}^{2 n} \\ x:=\left(\begin{array}{c} c \\ s \end{array}\right) \in \mathbb{R}^{2 n} \\ T:=\operatorname{diag}(\bar{T}, \bar{T}) \in \mathbb{R}^{2 n \times 2 n} \end{array}$$

对于前一步得到的矩阵形式优化目标，将$u$代入能量函数，转置标量，则优化目标变可变为

$$\begin{array}{rl} \min _{x \in \mathbb{R}^{2 n}} & x^{\top} Q x+2 x^{\top} v \\ \text { s.t. } & x^{\top} T x=A \end{array}$$

  使用拉格朗日乘子法得到

$$(Q-\lambda T) x=-v$$

将$x$看成关于$\lambda$的函数$x(\lambda)$,定义$g(\lambda):=x(\lambda)^{\top} T x(\lambda)-A$，则上述满足优化目标的乘子应为$g(\lambda)=0$的根，可使用二分法获得。

  证明：对于方程$(Q-\lambda T) x=-v$，假设$Q-\lambda T$不可逆，则必有$x$使

$$\begin{aligned}(Q-\lambda T) x&=0\\Qx&=\lambda Tx\end{aligned}$$

问题转化为广义特征值问题，设$\lambda_{min}$是其最小特征值。假设特征向量不正交于方程右边$v$，则对于方程左边，当$\lambda \rightarrow \lambda_{\min }$时，$\|x\| \rightarrow \infty$，即$\lim _{\lambda \rightarrow \lambda_{\min }} g(\lambda)=\infty$。同样的，当$\lambda \rightarrow -\infty$时，$\|x\| \rightarrow 0$，即

$\lim _{\lambda \rightarrow-\infty} g(\lambda)=-A$。又因为$g^{\prime}(\lambda)>0$,则在$\lambda\in(-\infty,\lambda_{min})$之间必定存在一个根使$g(\lambda) =0$。

  经上述步骤，优化的解为$x(\lambda_0)$，其中$g(\lambda_0) =0$。第一步求解$\lambda_{min}$时间很快，花费最大的是在第二部使用二分法求根(每次都要对一个稠密线性系统逆运算)。

7.内部场

  在求解内部场是可先单位化场$\frac{u(x)}{||u(x)||_2},x\in \partial \Omega$，在优化时是不能单位化的，不过在插值生成内部场时不同大小的$u$会造成坏的影响,比如$u(x)$越大，标架对于内部接近边界的奇异点的选择会更加显著。内部标架场可由边界元的公式获得,

$$u(x)=\int_{\partial \Omega}\left[G(y-x) \frac{\partial u(y)}{\partial \hat{n}}-u(y) \frac{\partial G(y-x)}{\partial \hat{n}}\right] \mathrm{d} y \quad \quad x \in \Omega \backslash \partial\Omega$$

对于每个三角形单元，定义如下

$$\begin{array}{l} \sigma_{k}(x):=\int_{T_{k}} G(y-x) \mathrm{d} y \\ \rho_{k}(x):=\hat{n}_{k} \cdot \int_{T_{k}} \nabla G(y-x) \mathrm{d} y \end{array}$$

则

$$u(x)=\sum_{k}\left[u_{k} \sigma_{k}(x)+[B u]_{k} \rho_{k}(x)\right]\\$$

这边貌似转换存在问题？按照定义应该是

$$u(x)=\sum_{k}\left[ \sigma_{k}(x)[B u]_k-u_{k}\rho_{k}(x)\right]$$

否则，按照他给定的式子，则原式变成了

$$u(x)=\int_{\partial \Omega}\left[u(y)G(y-x)+ \frac{\partial u(y)}{\partial \hat{n}} \frac{\partial G(y-x)}{\partial \hat{n}}\right] \mathrm{d} y \quad \quad x \in \Omega \backslash \partial\Omega$$

  解出$u$后，$u$可能不在解空间$\bar\Gamma$中，使用《Practical 3D Frame Field Generation》中梯度下降法(closest_frame)映射回$\bar \Gamma$再单位化。

  这里的closest_frame算法用的是$L_2$模，即欧式距离，能保证在$\Gamma$中欧式距离能给出很好的测度吗? （$\Gamma$是一个spherical 3- manifold）

8.奇异结构

  奇异结构通过采样细分，对内部采样三个点，若内部有奇异点，则四等分三角形，继续检测奇异点。

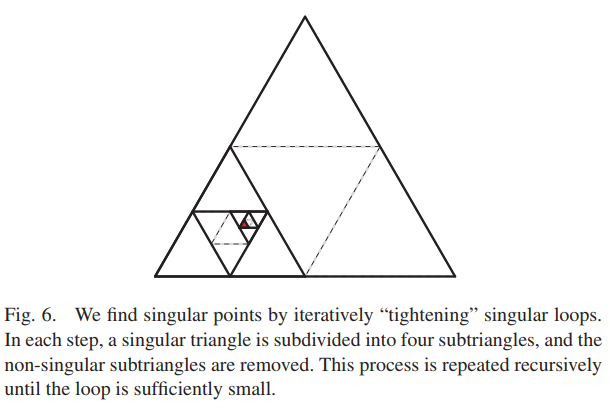
9.感想

• 之前几篇(包括这篇)的约束都在表面，而内部的奇异结构对六面体生成也是有影响的，因为这也是六面体相比于四面体网格难生成的原因(比如《Singularity-Constrained Octahedral Fields for Hexahedral Meshing》就有提到内部奇异结构的影响)。所以若要考虑六面体生成，仅保持表面约束法向约束是不是只是必要条件？
• 在求解标架场时，遇到的问题其一是非线性非凸约束（约束住$u$所代表的是基函数旋转后的系数），其二是得到的解需要映射回三维。对于一，大多是松弛约束，对于二，大多是采用梯度下降逆向求解。是否有更好的优化方法而不需要松弛约束和映射？