1.概括

  枚举了所有六面体网格中关于边的度的局部属性；推广了Hopf-Poincare index formula至octahedral fields;设计了一个通过求解非线性整形优化从一个预输入的奇异结构图生成一个优化后的octahedral field的算法。

2.拓扑关系

2.1 Local Topology of Eages

$$ \operatorname{idx}(e)=\left\{\begin{array}{ll}\left(4-\operatorname{val}_{h}(e)\right) / 4 & \text { for interior } e \\ \left(2-\operatorname{val}_{h}(e)\right) / 4 & \text { for boundary } e\end{array}\right. $$ 对于内部边，我们希望的是$$I_{interior}=\{\frac{1}{4},0,-\frac{1}{4}\}$$，即边的度为3、4、5；对于外部边，则为$$I_{boundary}=\{\frac{1}{4},0,-\frac{1}{4},-\frac{1}{2}\}$$,即度为1、2、3、4，而对于其他的index,则可以通过插入模板来修改，如下

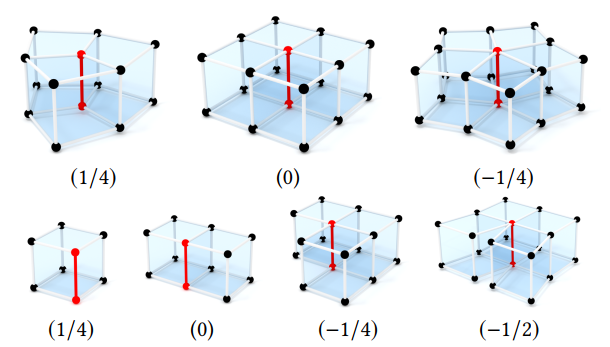
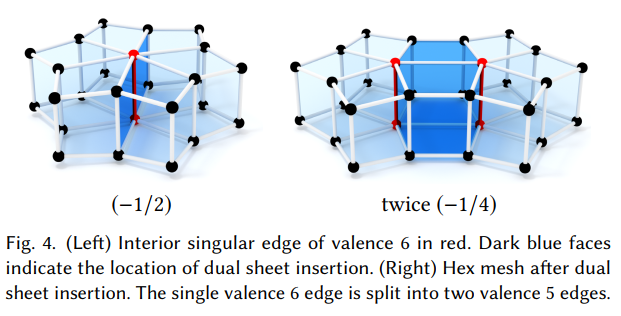
2.2 Local Topology of Vertex

  在CubeCover的论文中，有提到关于六面体网格中点拓扑的关系式，其用一个球包围该顶点，则连接该点的边在球上相交于一些点，连接这些点，形成三角形，则每个三角形对应一个六面体，如下

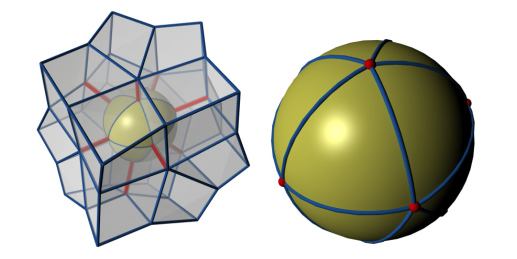
则根据欧拉公式$V-E+F=2$,以及面和边的关系$3F=2E$，以及点的度和边的关系$\sum_{v\in V}deg (v)=2E$，

则有如下关系

$$\sum_{v \in V }(6-deg(v))=12$$

以上关系式中，顶点的度其实对应的是六面体网格中边的度，同时可以观察出，边的度若为6，其不做贡献。若设$i,j,k$分别为球上度为$3、4、5$的点的数量，则有$3i+2j+k=12$,又因为$i+j+k=V$,则可穷举出如下的11个解

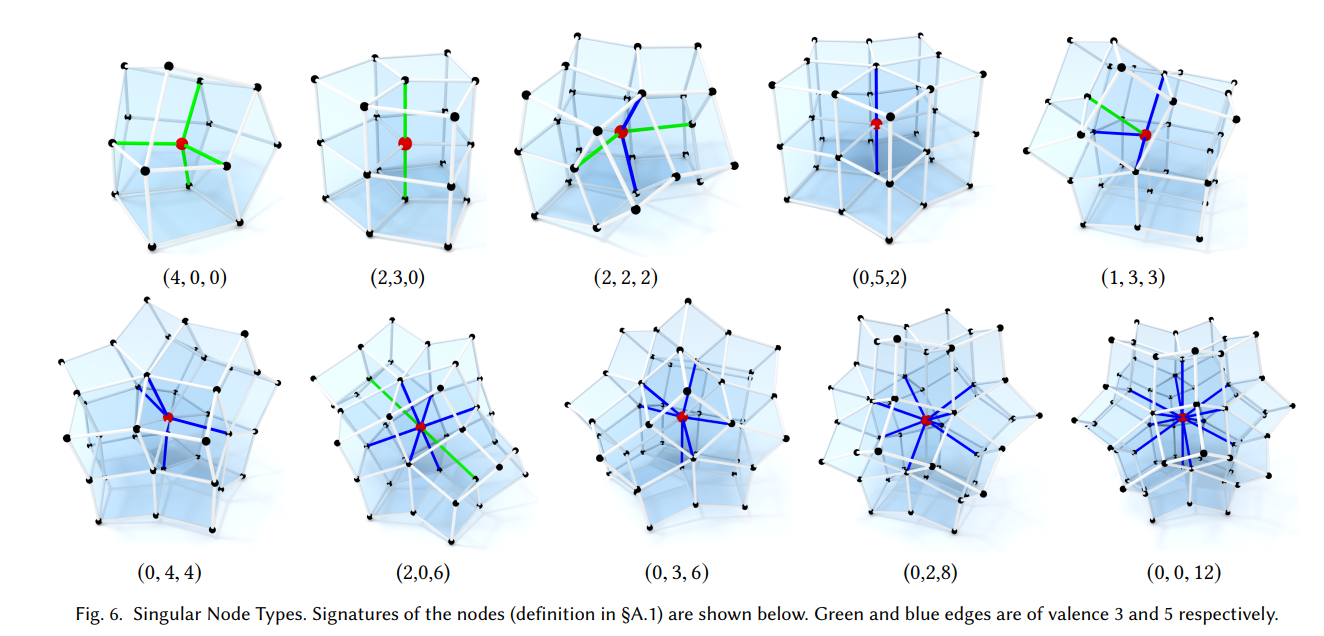
上图中为11中情况的10种，剩下的未标出1种是标准的立方体块的情况$(0,6,0)$。

2.3 全局条件

$$\sum_{v \in \partial V_{S}} \frac{1}{2}\left(1-\frac{\operatorname{val}_{h}(v)}{4}\right)-\sum_{e \in \partial E_{S}^{-}} \mathrm{idx}(e) +\sum_{v \in{V}^{'}_{S}}\left(1-\frac{\operatorname{val}_{h}(v)}{8}\right)-\sum_{e \in{E}_{S}^{'-}} \operatorname{idx}(e)=0$$

其中$\partial V_s,\partial V^{'}_{s}$分别为边界和内部的奇异图上的点，$\partial E^{-}_s,\partial E^{’-}_s$分别为不封闭的边界和不封闭的内部边。

3.Integer-Grid Maps（IGM）

  通常，标架场生成六面体网格的思路是将其映射到一个参数域

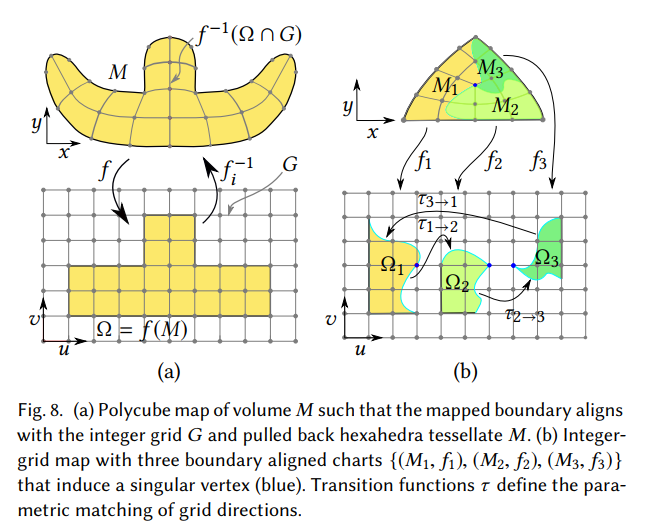
这里新的一种观点是，一个IGM可以诱导出一个field,但是相反的，不是任一个field可以转换成一个IGM,如果这个field可以，则说明这个field是globally hex-meshable。

4.Singularity Graph to Octahedral Field

4.1 Singularity Graph Constraints

4.1.1 Boundary alignment

  边界法向对齐标架

4.1.2 Singular arc alignment

  奇异边周围的标架之一与边相切

4.1.3 Edge type

  edge的one-ring cells 中的标架的matching matrix 的乘积

4.1.4 Vertex type

• Tangent continuity
• Corner constraint
• Boundary sector constraint